Locally Interacting Markov Chains Explained
Locally Interacting Markov Chains (LIMCs) are a powerful framework in probability theory and machine learning, offering efficient solutions for modeling complex systems. By focusing on local interactions, LIMCs simplify large-scale Markov Chain simulations, making them ideal for applications like network analysis, optimization, and sampling. This post explores their mechanics, benefits, and real-world applications, providing a clear understanding of how LIMCs work and why they matter. (Markov Chains, Probabilistic Models, Machine Learning)
What Are Locally Interacting Markov Chains?

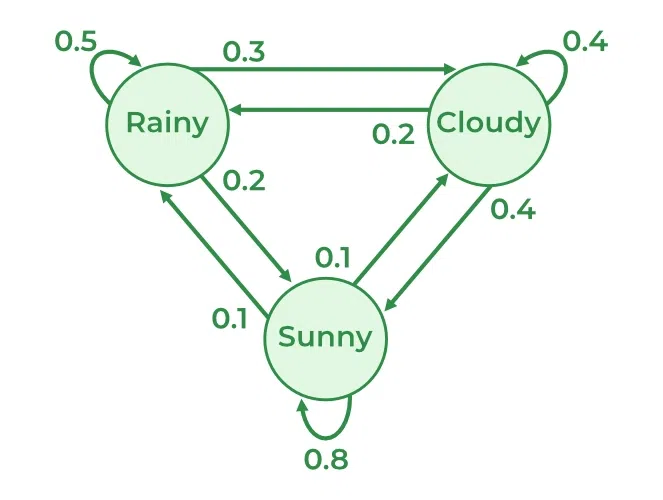
Locally Interacting Markov Chains (LIMCs) are a specialized type of Markov Chain where transitions depend only on the state of neighboring elements, rather than the entire system. This localized approach reduces computational complexity, enabling efficient simulations of large-scale systems. LIMCs are particularly useful in scenarios where global interactions are impractical or resource-intensive. (Markov Chains, Local Interactions, Computational Efficiency)
How Do Locally Interacting Markov Chains Work?
Key Components of LIMCs
- Local Transition Probabilities: Each state transitions based on its immediate neighbors, not the entire system.
- Decentralized Updates: Changes occur independently in different parts of the system, improving parallelism.
- Scalability: The localized nature allows LIMCs to handle large systems without exponential growth in complexity.
Steps in Implementing LIMCs
- Define the system as a graph with nodes representing states and edges representing local interactions.
- Assign transition probabilities based on neighboring states.
- Simulate the chain by updating states in parallel, respecting local dependencies.
📌 Note: LIMCs are best suited for systems where global interactions are not critical, such as in distributed computing or social network dynamics. (Graph Theory, Parallel Computing, Transition Probabilities)
Applications of Locally Interacting Markov Chains

LIMCs have diverse applications across fields:
| Field | Application |
|---|---|
| Machine Learning | Efficient sampling for Bayesian inference |
| Network Analysis | Modeling information spread in social networks |
| Optimization | Solving large-scale combinatorial problems |

Their scalability makes them invaluable for tackling real-world challenges in data science and engineering. (Bayesian Inference, Social Networks, Combinatorial Optimization)
Advantages and Limitations of LIMCs

Advantages
- Scalability: Handles large systems efficiently.
- Parallelization: Enables faster computations through decentralized updates.
- Simplicity: Easier to implement compared to global Markov Chains.
Limitations
- Locality Constraints: May not capture global dependencies accurately.
- Convergence Issues: Slower convergence in some complex systems.
Understanding these trade-offs helps in selecting the right model for specific use cases. (Scalability, Parallelization, Convergence)
Locally Interacting Markov Chains offer a balance between computational efficiency and modeling accuracy, making them a valuable tool in probabilistic modeling and machine learning. By focusing on local interactions, they simplify complex systems and enable scalable solutions. Whether you're working on network analysis, optimization, or Bayesian inference, LIMCs provide a robust framework for tackling real-world challenges. (Probabilistic Modeling, Scalable Solutions, Bayesian Inference)
What makes Locally Interacting Markov Chains different from standard Markov Chains?
+
LIMCs focus on local interactions, reducing computational complexity, while standard Markov Chains consider global transitions, which can be resource-intensive for large systems. (Markov Chains, Local Interactions)
Can LIMCs be used for global optimization problems?
+
Yes, but their effectiveness depends on the problem’s structure. LIMCs are better suited for problems with localized dependencies. (Global Optimization, Localized Dependencies)
How do LIMCs handle parallel computing?
+
LIMCs allow decentralized updates, enabling parallel computations across different parts of the system, which speeds up simulations. (Parallel Computing, Decentralized Updates)

