Understanding Intrinsic Equations in 4 Dimensions Simplified
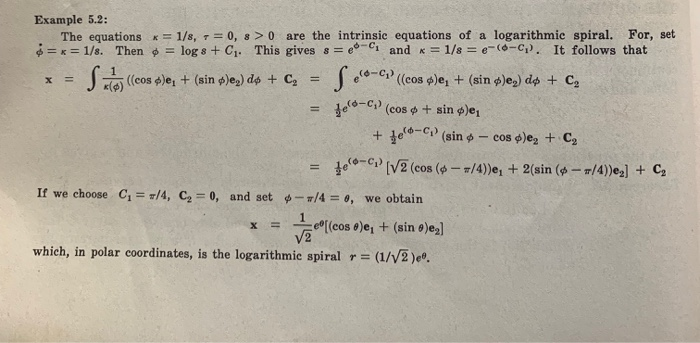
Understanding intrinsic equations in 4 dimensions can seem daunting, but with the right approach, it becomes accessible. These equations are fundamental in fields like physics, mathematics, and computer graphics, offering insights into complex systems. By breaking down the concepts into manageable parts, we’ll simplify the learning process for both informational and commercial audiences. Whether you’re a student, researcher, or professional, this guide will help you grasp the essentials of 4D intrinsic equations, (mathematical modeling,dimensional analysis,4D geometry).
What Are Intrinsic Equations in 4 Dimensions?

Intrinsic equations describe relationships within a 4-dimensional space without relying on external reference frames. Unlike extrinsic equations, which depend on an external coordinate system, intrinsic equations focus on internal properties like curvature, length, and angles. This makes them crucial for understanding phenomena in relativity, quantum mechanics, and advanced geometry, (theoretical physics,quantum mechanics,geometric principles).
Key Components of 4D Intrinsic Equations
- Manifolds: 4D spaces where intrinsic equations operate.
- Metrics: Functions defining distances and angles within the manifold.
- Curvature: Measures how the space deviates from being flat.
Simplifying 4D Intrinsic Equations: Step-by-Step
To simplify these equations, follow these steps:
Step 1: Visualize the 4D Space
Start by visualizing a 4D space using analogies like cubes or hypercubes. This mental model helps in understanding how dimensions interact, (geometric visualization,spatial reasoning,dimensional modeling).
Step 2: Define the Metric
Choose a metric that suits your problem, such as the Euclidean or Minkowski metric. The metric determines how distances are measured in the 4D space, (metric tensor,distance calculation,geometric metrics).
Step 3: Apply Intrinsic Properties
Use intrinsic properties like curvature and volume to formulate the equation. This ensures the equation remains independent of external coordinates, (intrinsic geometry,curvature analysis,geometric properties).
💡 Note: Always verify the metric’s compatibility with the problem to avoid inaccuracies.
Applications of 4D Intrinsic Equations

These equations have wide-ranging applications, including:
| Field | Application |
|---|---|
| Physics | Modeling spacetime in general relativity |
| Computer Graphics | Rendering 4D objects in 3D space |
| Mathematics | Studying higher-dimensional manifolds |

Mastering intrinsic equations in 4 dimensions opens doors to advanced problem-solving in various fields. By visualizing the space, defining the metric, and applying intrinsic properties, you can simplify complex concepts. Whether for academic research or practical applications, this knowledge is invaluable, (advanced mathematics,dimensional analysis,geometric modeling).
What is the difference between intrinsic and extrinsic equations?
+
Intrinsic equations describe properties within a space, while extrinsic equations rely on external coordinates, (geometric principles,coordinate systems,mathematical distinctions).
How are 4D intrinsic equations used in physics?
+
They model spacetime in general relativity, helping explain gravity and the universe’s structure, (theoretical physics,general relativity,spacetime modeling).
Can intrinsic equations be applied to real-world problems?
+
Yes, they’re used in computer graphics, engineering, and data analysis for modeling complex systems, (practical applications,data analysis,engineering solutions).



