Exploring Deterministic Finite Automata: Key Papers and Insights

Exploring Deterministic Finite Automata: Key Papers and Insights
Deterministic Finite Automata (DFA) are fundamental concepts in computer science, particularly in the study of formal languages and automata theory. Understanding DFAs is crucial for anyone delving into theoretical computer science, compiler design, or even software engineering. This blog post explores key papers, insights, and practical applications of DFAs, tailored for both informational and commercial audiences.
What is a Deterministic Finite Automaton?
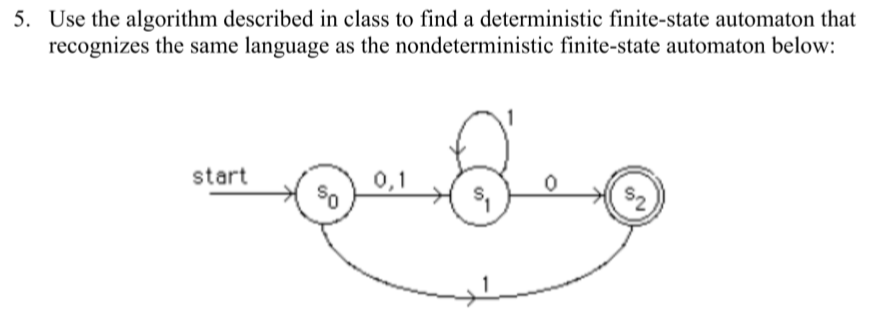
A Deterministic Finite Automaton (DFA) is a theoretical machine that recognizes patterns within input through a finite number of states. It processes input symbols one by one, transitioning between states based on predefined rules. DFAs are deterministic, meaning their next state is uniquely determined by the current state and input symbol. This simplicity makes them a cornerstone in automata theory, widely used in text processing, lexical analysis, and pattern matching. (Automata Theory, Formal Languages, Pattern Matching)
Key Papers Shaping DFA Research
Several seminal papers have shaped our understanding of DFAs. Below are some must-reads:
- Michael O. Rabin and Dana Scott (1959): Their work on finite automata and their decision problems laid the foundation for modern automata theory.
- John E. Hopcroft and Jeffrey D. Ullman (1979): Their book Introduction to Automata Theory, Languages, and Computation remains a classic, offering comprehensive insights into DFAs and related topics.
- Alfred V. Aho, Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman (2007): Compilers: Principles, Techniques, and Tools highlights the practical application of DFAs in lexical analysis.
📌 Note: These papers are essential for both academic research and practical implementation of DFAs.
Practical Applications of DFAs

DFAs are not just theoretical constructs; they have real-world applications:
- Lexical Analysis: DFAs are used in compilers to tokenize input strings, identifying keywords, identifiers, and operators.
- Pattern Matching: Tools like grep use DFAs to efficiently search for patterns in text.
- Protocol Analysis: In networking, DFAs help validate data packets against predefined protocols.
Building a DFA: Step-by-Step
Creating a DFA involves the following steps:
- Define the Problem: Identify the language or pattern the DFA should recognize.
- Construct States: Determine the finite set of states required.
- Define Transitions: Map input symbols to state transitions.
- Identify Accepting States: Specify which states indicate successful pattern recognition.
💡 Note: Use tools like JFLAP or Automaton Simulator for visualizing and testing your DFA.
DFA Minimization: Optimizing Efficiency

Minimizing a DFA reduces the number of states, making it more efficient. Key techniques include:
- State Partitioning: Group indistinguishable states together.
- Hopcroft’s Algorithm: A popular method for DFA minimization.
Checklist for DFA Implementation
- [ ] Define the language or pattern to recognize.
- [ ] Construct the initial set of states.
- [ ] Map transitions for each input symbol.
- [ ] Identify accepting states.
- [ ] Minimize the DFA for optimal performance.
DFA Tools and Resources
For those looking to implement or study DFAs, here are some valuable resources:
| Tool/Resource | Purpose |
|---|---|
| JFLAP | DFA simulation and visualization. |
| Automaton Simulator | Test and debug DFAs interactively. |
| Stanford CoreNLP | Practical DFA usage in NLP tasks. |

To summarize, Deterministic Finite Automata are a powerful tool in computer science, with applications ranging from theoretical research to practical software development. By exploring key papers and understanding their construction and optimization, you can harness the full potential of DFAs in your projects. (Automata Theory, Lexical Analysis, Pattern Matching)
What is the difference between DFA and NFA?
+
A DFA (Deterministic Finite Automaton) has a unique transition for each state and input symbol, while an NFA (Nondeterministic Finite Automaton) can have multiple transitions or ε-transitions.
How are DFAs used in compilers?
+
DFAs are used in the lexical analysis phase of compilers to tokenize input strings, identifying keywords, identifiers, and operators.
Can DFAs recognize all types of languages?
+
DFAs can only recognize regular languages, a subset of formal languages defined by regular expressions.

